MATLABDiffEq.jl is a common interface binding for the MATLAB ordinary differential equation solvers. It uses the MATLAB.jl interop in order to send the differential equation over to MATLAB and solve it. Note that this package requires the differential equation function to be defined using ParameterizedFunctions.jl.
Note that this package isn't for production use and is mostly just for benchmarking and helping new users migrate models over to Julia. For more efficient solvers, see the DifferentialEquations.jl documentation.
To install MATLABDiffEq.jl, use the following:
using Pkg
Pkg.add("MATLABDiffEq")MATLABDiffEq.jl is simply a solver on the DiffEq common interface, so for details see the DifferentialEquations.jl documentation.
However, the only options implemented are those for error calculations
(timeseries_error), saveat and tolerances.
Note that the algorithms are defined to have the same name as the MATLAB algorithms,
but are not exported. Thus to use ode45, you would specify the algorithm as
MATLABDiffEq.ode45().
using MATLABDiffEq, ParameterizedFunctions
f = @ode_def LotkaVolterra begin
dx = 1.5x - x*y
dy = -3y + x*y
end
tspan = (0.0,10.0)
u0 = [1.0,1.0]
prob = ODEProblem(f,u0,tspan)
sol = solve(prob,MATLABDiffEq.ode45())
function lorenz(du,u,p,t)
du[1] = 10.0(u[2]-u[1])
du[2] = u[1]*(28.0-u[3]) - u[2]
du[3] = u[1]*u[2] - (8/3)*u[3]
end
u0 = [1.0;0.0;0.0]
tspan = (0.0,100.0)
prob = ODEProblem(lorenz,u0,tspan)
sol = solve(prob,MATLABDiffEq.ode45())To measure the overhead of over the wrapper, note that the variables from the session will be still stored in MATLAB after the computation is done. Thus you can simply call the same ODE function and time it directly. This is done by:
@time MATLABDiffEq.eval_string("[t,u] = $(algstr)(diffeqf,tspan,u0,options);")To be even more pedantic, you can play around in the actual MATLAB session by using
MATLABDiffEq.show_msession()
Generally, for long enough problems the overhead is minimal. Example:
using DiffEqBase, ParameterizedFunctions, MATLABDiffEq
f = @ode_def_bare RigidBodyBench begin
dy1 = -2*y2*y3
dy2 = 1.25*y1*y3
dy3 = -0.5*y1*y2 + 0.25*sin(t)^2
end
prob = ODEProblem(f,[1.0;0.0;0.9],(0.0,100.0))
alg = MATLABDiffEq.ode45()
algstr = string(typeof(alg).name.name)For this, we get the following:
julia> @time sol = solve(prob,alg);
0.063918 seconds (38.84 k allocations: 1.556 MB)
julia> @time sol = solve(prob,alg);
0.062600 seconds (38.84 k allocations: 1.556 MB)
julia> @time sol = solve(prob,alg);
0.061438 seconds (38.84 k allocations: 1.556 MB)
julia> @time sol = solve(prob,alg);
0.065460 seconds (38.84 k allocations: 1.556 MB)
julia> @time MATLABDiffEq.eval_string("[t,u] = $(algstr)(diffeqf,tspan,u0,options);")
0.058249 seconds (11 allocations: 528 bytes)
julia> @time MATLABDiffEq.eval_string("[t,u] = $(algstr)(diffeqf,tspan,u0,options);")
0.060367 seconds (11 allocations: 528 bytes)
julia> @time MATLABDiffEq.eval_string("[t,u] = $(algstr)(diffeqf,tspan,u0,options);")
0.060171 seconds (11 allocations: 528 bytes)
julia> @time MATLABDiffEq.eval_string("[t,u] = $(algstr)(diffeqf,tspan,u0,options);")
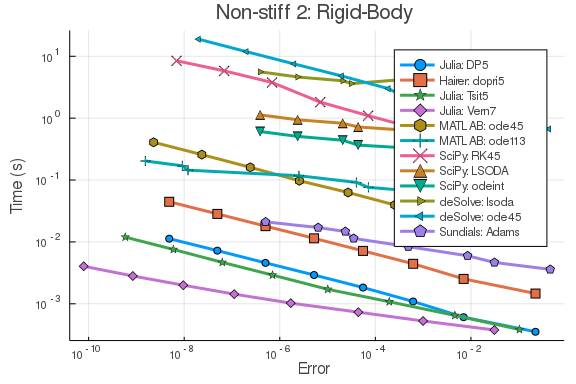
0.058928 seconds (11 allocations: 528 bytes)The following benchmarks demonstrate a 100x performance advantage for the pure-Julia methods over the MATLAB ODE solvers across a range of stiff and non-stiff ODEs. These were ran with Julia 1.2, MATLAB 2019B, deSolve 1.2.5, and SciPy 1.3.1 after verifying negligible overhead on interop. Note that the MATLAB solvers do outperform that of Python and R.
f = @ode_def_bare LotkaVolterra begin
dx = a*x - b*x*y
dy = -c*y + d*x*y
end a b c d
p = [1.5,1,3,1]
tspan = (0.0,10.0)
u0 = [1.0,1.0]
prob = ODEProblem(f,u0,tspan,p)
sol = solve(prob,Vern7(),abstol=1/10^14,reltol=1/10^14)
test_sol = TestSolution(sol)
setups = [Dict(:alg=>DP5())
Dict(:alg=>dopri5())
Dict(:alg=>Tsit5())
Dict(:alg=>Vern7())
Dict(:alg=>MATLABDiffEq.ode45())
Dict(:alg=>MATLABDiffEq.ode113())
Dict(:alg=>SciPyDiffEq.RK45())
Dict(:alg=>SciPyDiffEq.LSODA())
Dict(:alg=>SciPyDiffEq.odeint())
Dict(:alg=>deSolveDiffEq.lsoda())
Dict(:alg=>deSolveDiffEq.ode45())
Dict(:alg=>CVODE_Adams())
]
names = [
"Julia: DP5"
"Hairer: dopri5"
"Julia: Tsit5"
"Julia: Vern7"
"MATLAB: ode45"
"MATLAB: ode113"
"SciPy: RK45"
"SciPy: LSODA"
"SciPy: odeint"
"deSolve: lsoda"
"deSolve: ode45"
"Sundials: Adams"
]
abstols = 1.0 ./ 10.0 .^ (6:13)
reltols = 1.0 ./ 10.0 .^ (3:10)
wp = WorkPrecisionSet(prob,abstols,reltols,setups;
names = names,
appxsol=test_sol,dense=false,
save_everystep=false,numruns=100,maxiters=10000000,
timeseries_errors=false,verbose=false)
plot(wp,title="Non-stiff 1: Lotka-Volterra")f = @ode_def_bare RigidBodyBench begin
dy1 = -2*y2*y3
dy2 = 1.25*y1*y3
dy3 = -0.5*y1*y2 + 0.25*sin(t)^2
end
prob = ODEProblem(f,[1.0;0.0;0.9],(0.0,100.0))
sol = solve(prob,Vern7(),abstol=1/10^14,reltol=1/10^14)
test_sol = TestSolution(sol)
setups = [Dict(:alg=>DP5())
Dict(:alg=>dopri5())
Dict(:alg=>Tsit5())
Dict(:alg=>Vern7())
Dict(:alg=>MATLABDiffEq.ode45())
Dict(:alg=>MATLABDiffEq.ode113())
Dict(:alg=>SciPyDiffEq.RK45())
Dict(:alg=>SciPyDiffEq.LSODA())
Dict(:alg=>SciPyDiffEq.odeint())
Dict(:alg=>deSolveDiffEq.lsoda())
Dict(:alg=>deSolveDiffEq.ode45())
Dict(:alg=>CVODE_Adams())
]
names = [
"Julia: DP5"
"Hairer: dopri5"
"Julia: Tsit5"
"Julia: Vern7"
"MATLAB: ode45"
"MATLAB: ode113"
"SciPy: RK45"
"SciPy: LSODA"
"SciPy: odeint"
"deSolve: lsoda"
"deSolve: ode45"
"Sundials: Adams"
]
abstols = 1.0 ./ 10.0 .^ (6:13)
reltols = 1.0 ./ 10.0 .^ (3:10)
wp = WorkPrecisionSet(prob,abstols,reltols,setups;
names = names,
appxsol=test_sol,dense=false,
save_everystep=false,numruns=100,maxiters=10000000,
timeseries_errors=false,verbose=false)
plot(wp,title="Non-stiff 2: Rigid-Body")rober = @ode_def begin
dy₁ = -k₁*y₁+k₃*y₂*y₃
dy₂ = k₁*y₁-k₂*y₂^2-k₃*y₂*y₃
dy₃ = k₂*y₂^2
end k₁ k₂ k₃
prob = ODEProblem(rober,[1.0,0.0,0.0],(0.0,1e5),[0.04,3e7,1e4])
sol = solve(prob,CVODE_BDF(),abstol=1/10^14,reltol=1/10^14)
test_sol = TestSolution(sol)
abstols = 1.0 ./ 10.0 .^ (7:8)
reltols = 1.0 ./ 10.0 .^ (3:4);
setups = [Dict(:alg=>Rosenbrock23())
Dict(:alg=>TRBDF2())
Dict(:alg=>RadauIIA5())
Dict(:alg=>rodas())
Dict(:alg=>radau())
Dict(:alg=>MATLABDiffEq.ode23s())
Dict(:alg=>MATLABDiffEq.ode15s())
Dict(:alg=>SciPyDiffEq.LSODA())
Dict(:alg=>SciPyDiffEq.BDF())
Dict(:alg=>SciPyDiffEq.odeint())
Dict(:alg=>deSolveDiffEq.lsoda())
Dict(:alg=>CVODE_BDF())
]
names = [
"Julia: Rosenbrock23"
"Julia: TRBDF2"
"Julia: radau"
"Hairer: rodas"
"Hairer: radau"
"MATLAB: ode23s"
"MATLAB: ode15s"
"SciPy: LSODA"
"SciPy: BDF"
"SciPy: odeint"
"deSolve: lsoda"
"Sundials: CVODE"
]
wp = WorkPrecisionSet(prob,abstols,reltols,setups;
names = names,print_names = true,
dense=false,verbose = false,
save_everystep=false,appxsol=test_sol,
maxiters=Int(1e5))
plot(wp,title="Stiff 1: ROBER", legend=:topleft)f = @ode_def Hires begin
dy1 = -1.71*y1 + 0.43*y2 + 8.32*y3 + 0.0007
dy2 = 1.71*y1 - 8.75*y2
dy3 = -10.03*y3 + 0.43*y4 + 0.035*y5
dy4 = 8.32*y2 + 1.71*y3 - 1.12*y4
dy5 = -1.745*y5 + 0.43*y6 + 0.43*y7
dy6 = -280.0*y6*y8 + 0.69*y4 + 1.71*y5 -
0.43*y6 + 0.69*y7
dy7 = 280.0*y6*y8 - 1.81*y7
dy8 = -280.0*y6*y8 + 1.81*y7
end
u0 = zeros(8)
u0[1] = 1
u0[8] = 0.0057
prob = ODEProblem(f,u0,(0.0,321.8122))
sol = solve(prob,Rodas5(),abstol=1/10^14,reltol=1/10^14)
test_sol = TestSolution(sol)
abstols = 1.0 ./ 10.0 .^ (5:8)
reltols = 1.0 ./ 10.0 .^ (1:4);
setups = [Dict(:alg=>Rosenbrock23())
Dict(:alg=>TRBDF2())
Dict(:alg=>RadauIIA5())
Dict(:alg=>rodas())
Dict(:alg=>radau())
Dict(:alg=>MATLABDiffEq.ode23s())
Dict(:alg=>MATLABDiffEq.ode15s())
Dict(:alg=>SciPyDiffEq.LSODA())
Dict(:alg=>SciPyDiffEq.BDF())
Dict(:alg=>SciPyDiffEq.odeint())
Dict(:alg=>deSolveDiffEq.lsoda())
Dict(:alg=>CVODE_BDF())
]
names = [
"Julia: Rosenbrock23"
"Julia: TRBDF2"
"Julia: radau"
"Hairer: rodas"
"Hairer: radau"
"MATLAB: ode23s"
"MATLAB: ode15s"
"SciPy: LSODA"
"SciPy: BDF"
"SciPy: odeint"
"deSolve: lsoda"
"Sundials: CVODE"
]
wp = WorkPrecisionSet(prob,abstols,reltols,setups;
names = names,print_names = true,
save_everystep=false,appxsol=test_sol,
maxiters=Int(1e5),numruns=100)
plot(wp,title="Stiff 2: Hires",legend=:topleft)