-
Notifications
You must be signed in to change notification settings - Fork 636
Replication and Replication Guide Part 1
Replication and Replication Guide
- Replication and Replication Guide 1: Replication
- Replication and Replication Guide 2: Design for Replication
- Replication and Replication Guide 3: Replication Guide
One open problem in visual programming is how to represent iteration. As an iteration normally has a condition and an iteration body, representing it visually usually results in a large number of nodes with tangled connections. Visual programming researchers have come up with a lot of ideas to reduce cognitive overhead, but most solutions are still mimics of WHILE-loop or FOR-loop in normal programming languages. Users have to spent more time thinking about the details of iteration. In other words, user has to think about “how to do” instead of “what to do”.
For most practical purposes, Dynamo represents data in multidimensional lists. Most nodes in Dynamo (e.g. + node) are able to handle single values (e.g. 2 + 3) as well as multidimensional lists (e.g. { 2, 3 } + { 4, 5 }). In such case, iteration is not necessary. But there is a hidden requirement: one computation outcome shouldn’t affect the outcome of the other computation. This kind of iteration is called horizontally parallel iteration. In other words, it is about doing some operation for all elements in a set for a certain number of times where each operation runs independently. The good thing is that most iterations fall in this category.
The concept for a function that accepts single values can also accept array values is not something new. [APL] (https://en.wikipedia.org/wiki/APL_(programming_language)) is one of the earliest [array programming language] (https://en.wikipedia.org/wiki/Array_programming ). For Dynamo, this ability to accept a list in place of a single value is called replication, and it is built right in the heart of DesignScript -- the programming language that powers Dynamo.
Basically, replication is the unpacking of inputs of a node to a series of values that a node expects to work with. Therefore, the execution of the node will be expanded to a series of operations where all the results will then be aggregated and returned.
There are two kinds of replication modes. For a node f with a series of input xs1, xs2, ..., xsn,
-
Cartesian Replication iterates through all the elements in an input. For each element, node is executed with that element together with other inputs. Iteration is just for top level elements. For example, if we are going to iterate through
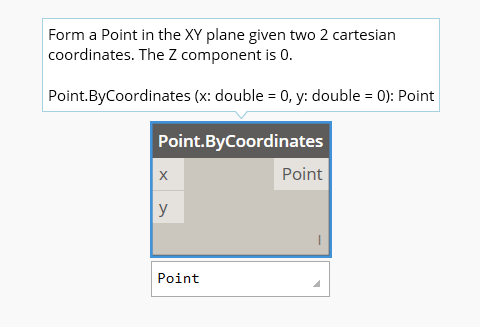
{{{1}, {2}}, {{3}, {4}}}, we iterate first element{{1}, {2}}and then the second element{{3}, {4}}. For users who have some Python experience, Cartesian replication can be expressed in the following Python list comprehension. Note the enclosing{}puts the result back into a list:{ f(x, xs2, ..., xsn) for x in xs1 }For example, in the following picture,
Point.ByCoordinatesreplicates on inputx. Note the result is still in a list.
-
Zip Replication iterates through two or more inputs simultaneously and executes the node with these elements together with other inputs. It can expressed in the following Python list comprehension (this case do zip replication on all inputs)
{ f(x1, x2, ..., xn) for x1, x2, ..., xn in zip(xs1, xs2, ..., xsn) }For example, in the following picture,
Point.ByCoordinatesdoes zip replication on inputs of x and y. Note the result is put in a list.
Note replication can be nested. That is, inside a Cartesian Replication we could do another Zip Replication or Cartesian Replication. Each replication creates an extra “layer”, or in Dynamo terms, a list.
Now you may ask, how does Dynamo decide whether to use replication or not? If replication is used, which of the two modes should be used?
The answer is in the signature of a node:
In the info bubble, Point.ByCoordinates(x: double = 0, y: double = 0, z: double = 0): Point specifies the kind of inputs that this node expects to work with. Here x: double specifies the expected type of input x (we call x a parameter). double is a type, means a double-precision floating-point value like 1.2, 3.14 and so on.
If a node expects to work with a one dimensional list of some type T (T can be any type like int, bool, Point, Line, etc), the type of that parameter would be T[]. Similarly, a two dimensional list of type T is T[][], a three dimensional list is T[][][] and so on. A special case is the arbitrary dimensional list, which is T[]..[]. In DesignScript terms, we call the dimension of a list its rank. So the rank of T is 0, the rank of T[] is 1, the rank of T[][] is 2 and the rank of T[]..[] is a special value called arbitrary rank.
Similarly, the real input (we call it argument) has a rank as well.
Replication depends on the difference between the rank of parameter that the node expects and the rank of real input (argument). It is computed in the following steps:
- Compute the rank delta
dk = rank of parameter at position k - rank of argument at position kfor each parameter and argument pair but skip those parameters that have arbitrary ranks (that is,[]..[]); then we get a list of delta ranks:{d1, d2, ..., dn}. - If there are two or more
dk > 0, do Zip Replication on all those arguments on the corresponding positions, and reducedkby 1 (that is,dk = dk - 1). Repeat this process until only one or nodk > 0. - If there is a
dk > 0, do Cartesian Replication on that argument and and reducedkby 1 (that is,dk = dk - 1). Repeat this process until no moredk > 0.
If you prefer to read code than text, the following pesudo-code shows this process:
while (two or more dk > 0)
{
Zip Replication on argument at position k for {dk | dk > 0}
for each dk, dk = dk - 1
}
while (any dk > 0)
{
Cartesian Replication on argument at position k
dk = dk - 1
}
Node: BoundingBox.ByGeometry(geometry: Geometry[])
- The rank of parameter
geometryis 1. - Input:
pts = {{p1, p2}, {p3, p4}}, the rank of argumentptsis 2.
Replication steps:
d(geometry) = 2 - 1 = 1- As there is only one parameter and
d(geometry) > 0, do Cartesian Replication onpts, which is equivalent to execute{BoundingBox.ByGeometry({p1, p2}), BoundingBox.ByGeometry({p3, p4})}.
Table below shows this process:

Node: Point.ByCoordinates(x: double, y: double)
- The rank of parameter
xis 0, the rank of parameteryis 0. - Input:
xs = {{1, 2}, {3, 4}}, ys = {5, 6}, so the rank of argumentxsis 2, the rank of argumentysis 1.
Replication steps:
{dx = 2 - 0 = 2, dy = 1 - 0 = 1}- As both rank delta values are larger than 0, do Zip Replication on
xsandysfirstly. It is equivalent to execute node with{Point.ByCoordinates({1, 2}, 5}, Point.ByCoordinates({3, 4}, 6)}. After this step,{dx = 2 - 1 = 1, dy = 1 - 1 = 0} - As there is only one rank delta value is larger than 0, do Cartesian Replication on the result that comes from step 2. That is, do Cartesian Replication on argument
{1, 2}forPoint.ByCoordinates({1, 2}, 5}and{3, 4}Pont.ByCoordinates({3, 4}, 6)from step 2.
Table below shows this process:

Define a function foo() showed below and call this function. Note the rank of y is arbitrary (that is, []..[]), so it will be excluded from replication computation.

Table below shows the replication computation process (dk = -1 means exclude this parameter from replication computation):

Looking for help with using the Dynamo application? Try dynamobim.org.
- Dynamo 2.0 Language Changes Explained
- How Replication and Replication Guide work: Part 1
- How Replication and Replication Guide work: Part 2
- How Replication and Replication Guide work: Part 3