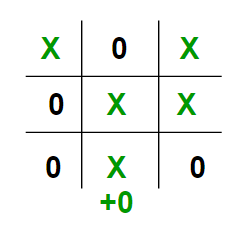-
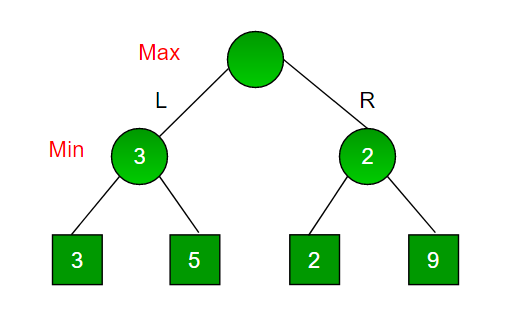
Minimax is a kind of backtracking algorithm to find the optimal move for a player, assuming that your opponent also plays optimally.
-
In Minimax the two players are called maximizer and minimizer. The maximizer tries to get the highest score possible while the minimizer tries to do the opposite and get the lowest score possible.
-
Every board state has a value associated with it. In a given state if the maximizer has upper hand then, the score of the board will tend to be some positive value. If the minimizer has the upper hand in that board state then it will tend to be some negative value.
-
Since this is a backtracking based algorithm, it tries all possible moves, then backtracks and makes a decision.
#include <bits\stdc++.h>
using namespace std;
int getLeftChild(int node) { return node * 2; }
int getRightChild(int node) { return node * 2 + 1; }
int minimax(int curDepth, int nodeIndex, bool isMaximizer, vector<int> scores, int h) {
if (curDepth == h) { // we finished the tree
return scores[nodeIndex];
}
if (isMaximizer) { // I am a maximizer node
int leftValue = minimax(curDepth + 1, getLeftChild(nodeIndex), false, scores, h);
int rightValue = minimax(curDepth + 1, getRightChild(nodeIndex), false, scores, h);
return max(leftValue, rightValue); // get max from my children
}
else {
int leftValue = minimax(curDepth + 1, getLeftChild(nodeIndex), true, scores, h);
int rightValue = minimax(curDepth + 1, getRightChild(nodeIndex), true, scores, h);
return min(leftValue, rightValue);
}
}
int main() {
vector<int> scores = { 3, 5, 2, 9, 12, 5, 23, 23 };
int n = scores.size();
int h = ceil(log2(n));
int maximizerValue = minimax(0, 0, true, scores, h);
cout << maximizerValue << endl; // 12
}-
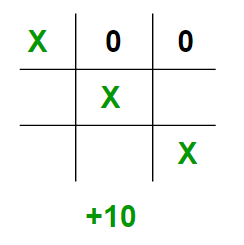
In the above example, the scores (leaves of Game Tree) are given to us. For a typical game, we need to derive these values by a function, This function is often known as Evaluation Function, It is sometimes also called Heuristic Function.
-
The basic idea behind the evaluation function is to give a high value for a board if maximizer‘s turn or a low value for the board if minimizer‘s turn.
-
let us consider X as the maximizer and O as the minimizer.
#include <bits\stdc++.h>
using namespace std;
const int maximizerValue = 10;
const int minimizerValue = -10;
int evaluate(char grid[3][3]) {
// check winning state in rows
for (int row = 0; row < 3; row++) {
if (grid[row][0] == grid[row][1] && grid[row][0] == grid[row][2]) {
if (grid[row][0] == 'x') return maximizerValue;
else if (grid[row][0] == 'o') return minimizerValue;
}
}
// check winning state in cols
for (int col = 0; col < 3; col++) {
if (grid[0][col] == grid[1][col] && grid[0][col] == grid[2][col]) {
if (grid[0][col] == 'x') return maximizerValue;
else if (grid[0][col] == 'o') return minimizerValue;
}
}
// check winning state in main diagonal
if (grid[0][0] == grid[1][1] && grid[0][0] == grid[2][2]) {
if (grid[0][0] == 'x') return maximizerValue;
else if (grid[0][0] == 'o') return minimizerValue;
}
// check winning state in anti diagonal
if (grid[0][2] == grid[1][1] && grid[1][1] == grid[2][0]) {
if (grid[0][2] == 'x') return maximizerValue;
else if (grid[0][2] == 'o') return minimizerValue;
}
return 0; // tie state
}
int main() {
// x for maximizer player
// o for minimizer player
// _ empty cell
char board[3][3] =
{
{ 'x', '_', 'o' },
{ '_', 'x', 'o' },
{ '_', '_', 'x' }
};
int evalValue = evaluate(board);
cout << evalValue << endl;
}- We shall be introducing a new function called findBestMove(). This function evaluates all the available moves using minimax() and then returns the best move the maximizer can make
function findBestMove(board):
bestMove = NULL
for each move in board :
if current move is better than bestMove
bestMove = current move
return bestMove
- To check whether or not the current move is better than the best move we take the help of minimax() function which will consider all the possible ways the game can go and returns the best value for that move, assuming the opponent also plays optimally
function minimax(board, depth, isMaximizingPlayer):
if current board state is a terminal state :
return value of the board
if isMaximizingPlayer :
bestVal = -INFINITY
for each move in board :
value = minimax(board, depth+1, false)
bestVal = max( bestVal, value)
return bestVal
else :
bestVal = +INFINITY
for each move in board :
value = minimax(board, depth+1, true)
bestVal = min( bestVal, value)
return bestVal
- To check whether the game is over and to make sure there are no moves left we use isMovesLeft() function
function isMovesLeft(board):
for each cell in board:
if current cell is empty:
return true
return false
-
Even though the following AI plays perfectly, it might choose to make a move which will result in a slower victory or a faster loss. Lets take an example and explain it.
-
Assume that there are 2 possible ways for X to win the game from a give board state.
- Move A : X can win in 2 move
- Move B : X can win in 4 moves
-
Our evaluation function will return a value of +10 for both moves A and B. Even though the move A is better because it ensures a faster victory, our AI may choose B sometimes.
-
To overcome this problem we subtract the depth value from the evaluated score. This means that in case of a victory it will choose a the victory which takes least number of moves and in case of a loss it will try to prolong the game and play as many moves as possible. So the new evaluated value will be
- Move A will have a value of +10 – 2 = 8
- Move B will have a value of +10 – 4 = 6
#include <bits\stdc++.h>
using namespace std;
const int maximizerValue = 10;
const int minimizerValue = -10;
const char player = 'x';
const char ai = 'o';
struct Move {
int row, col;
};
int evaluate(char grid[3][3]) {
// check winning state in rows
for (int row = 0; row < 3; row++) {
if (grid[row][0] == grid[row][1] && grid[row][0] == grid[row][2]) {
if (grid[row][0] == 'x') return maximizerValue;
else if (grid[row][0] == 'o') return minimizerValue;
}
}
// check winning state in cols
for (int col = 0; col < 3; col++) {
if (grid[0][col] == grid[1][col] && grid[0][col] == grid[2][col]) {
if (grid[0][col] == 'x') return maximizerValue;
else if (grid[0][col] == 'o') return minimizerValue;
}
}
// check winning state in main diagonal
if (grid[0][0] == grid[1][1] && grid[0][0] == grid[2][2]) {
if (grid[0][0] == 'x') return maximizerValue;
else if (grid[0][0] == 'o') return minimizerValue;
}
// check winning state in anti diagonal
if (grid[0][2] == grid[1][1] && grid[1][1] == grid[2][0]) {
if (grid[0][2] == 'x') return maximizerValue;
else if (grid[0][2] == 'o') return minimizerValue;
}
return 0; // tie state
}
bool isMoveLeft(char board[3][3]) {
for (int row = 0; row < 3; row++) {
for (int col = 0; col < 3; col++) {
if (board[row][col] == '_') return true;
}
}
return false;
}
int minimax(char board[3][3], int depth, int isMazimizer) {
int score = evaluate(board);
if (score == maximizerValue) return maximizerValue;
if (score == minimizerValue) return minimizerValue;
if (!isMoveLeft(board)) return 0;
// If this maximizer's move
if (isMazimizer)
{
int best = -1000;
// Traverse all cells
for (int row = 0; row<3; row++)
{
for (int col = 0; col<3; col++)
{
// Check if cell is empty
if (board[row][col] == '_')
{
// Make the move
board[row][col] = player;
// Call minimax recursively and choose
// the maximum value
best = max(best,
minimax(board, depth + 1, !isMazimizer));
// Undo the move
board[row][col] = '_';
}
}
}
return best;
}
// If this minimizer's move
else
{
int best = 1000;
// Traverse all cells
for (int row = 0; row<3; row++)
{
for (int col = 0; col<3; col++)
{
// Check if cell is empty
if (board[row][col] == '_')
{
// Make the move
board[row][col] = ai;
// Call minimax recursively and choose
// the minimum value
best = min(best,
minimax(board, depth + 1, !isMazimizer));
// Undo the move
board[row][col] = '_';
}
}
}
return best;
}
}
Move findBestMove(char board[3][3]) {
int bestVal = INT_MIN;
Move bestMove;
bestMove.row = -1;
bestMove.col = -1;
for (int row = 0; row < 3; row++) {
for (int col = 0; col < 3; col++) {
// Check if cell is empty
if (board[row][col] == '_') {
// Make the move
board[row][col] = player;
int moveValue = minimax(board, 0, false);
if (moveValue > bestVal) {
bestVal = moveValue;
bestMove.row = row;
bestMove.col = col;
}
}
}
}
cout << "The value of the best move is : " << bestVal << endl;
return bestMove;
}
int main() {
// x for maximizer player
// o for minimizer player
// _ empty cell
char board[3][3] =
{
{ 'x', 'o', 'x' },
{ 'o', 'o', 'x' },
{ '_', '_', '_' }
};
Move bestMove = findBestMove(board);
cout << "The Optimal Move is : " << endl;
cout << bestMove.row << ' ' << bestMove.col << endl;
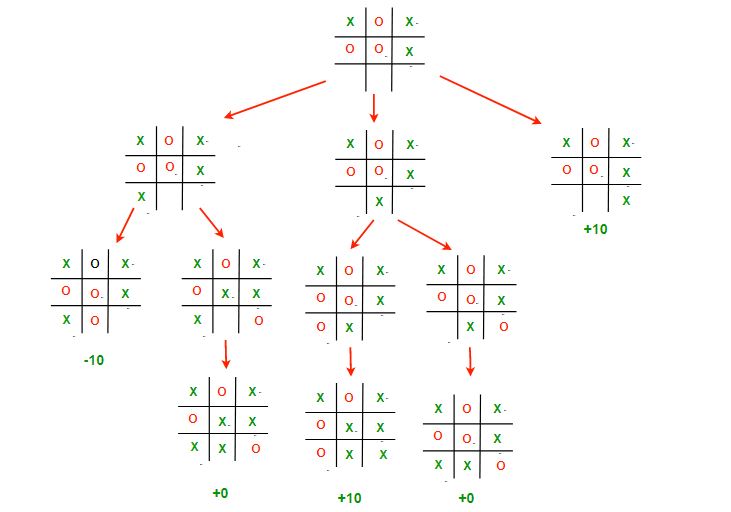
}- This image depicts all the possible paths that the game can take from the root board state. It is often called the Game Tree