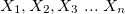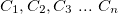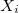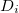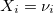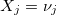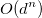12-ConstraintSatisfactionProblems

Constraint Satisfaction Problems

The problems of this category usually require the states and goal test to conform to a standard, structured and very simple representation.

Definitions

• A CSP is defined by
  • a set of variables
  • a set of contraints given by . In this setup there can be three categories of constraints:
    • asd
  • each variable has a non empty domain of possible values.
• A state of the problem is defined by assignment of values to some or all of the variables {, , ...}.
• An assignment that does not violate any constraints is called a consistent or legal assignment.
• A complete assignment is the one, in which all variables of a CSP are mentioned.
• A complete and consistent assignment is called a solution for any given CSP.

Note: Although the above process is in reference to assignment problems, some CSVs could also require solutions to maximize an objective function. The underlying principles would still remain the same

Structure

1. The simplest kind of CSPs are the ones with discrete and finite domains. Map coloring problems and 8-Queens problems are the popular ones of this kind. In case of a problem with domain size d and number of variables n, the total number of possible and complete assignments is .

   This goes on to show that in the worst case scenario, we will not be able to solve finite-domain CSPs in less than exponential time.

2. There can be problems where the domain for a variable.

Solving Mechanism

It is interesting to see that the a CSP can be given an incremental formulation as a standard search problem using the following intuitive procedure:

1. Initial State: the empty assignment {}, in which all variables are unassigned
2. Successor Function: A value can be assigned to any variable provided that it does not conflict with any previously assigned variables
3. Goal Test: The current assignment is complete
4. Path Cost: a constant cost (eg. 1) for every step

Every solution must be a complete assignment, therefore appears appears at depth n if there are n variables. Due to this property depth first search algorithms are really popular for CSPs.

It is also noteworthy that the path taken for reaching a particular solution is irrelevant to the final outcome. Therefore another way to tackle this problem could be to make sure that every state is a complete assignment which might or might not satisfy the constraints and then use local search methods to find solutions.